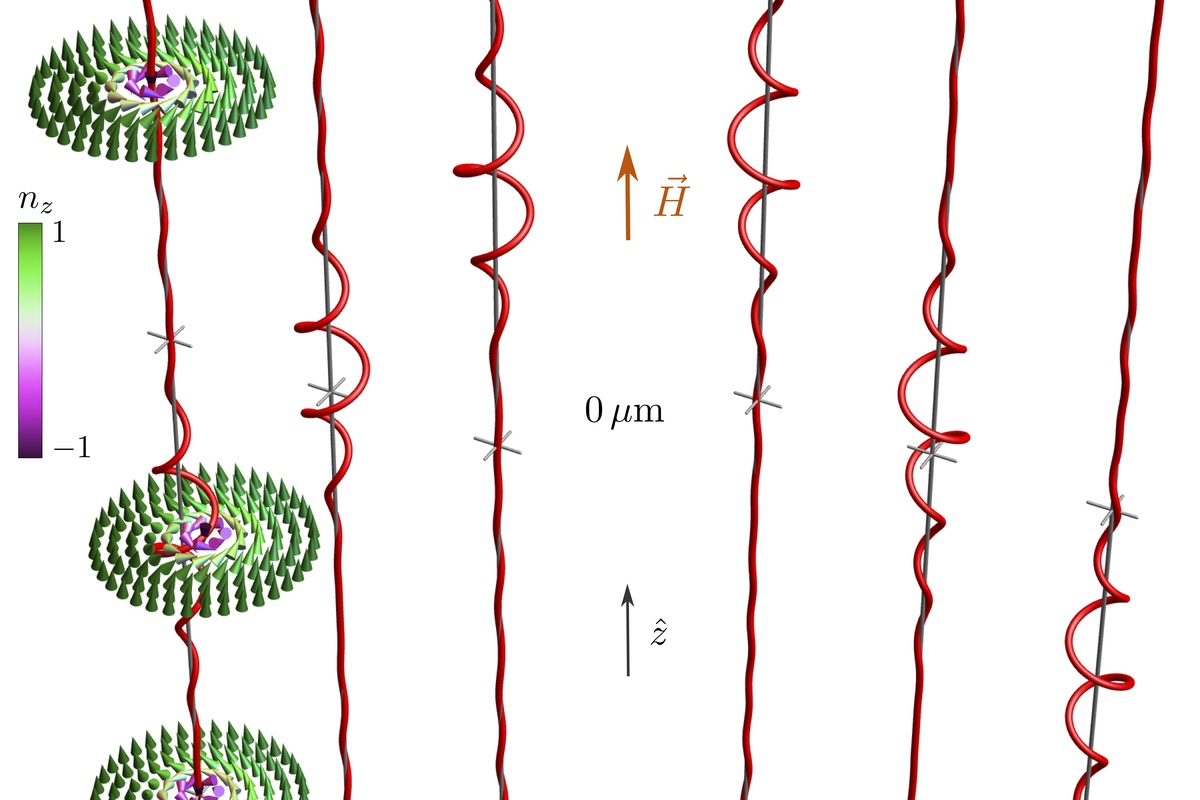
Research: Solitary waves on skyrmion strings
Effective one-dimensional strings can be found in diverse systems such as domain walls in magnetic films, vortex filaments in classical as well as quantum fluids, or cosmic strings in the universe. These strings can elastically bend and twist, and this elasticity also determines their dynamical behaviour at low energies. This results in collective low-amplitude excitations, for example, Kelvin waves in fluids that were studied by Lord Kelvin already in the 19th century. Such waves propagate along vortex filaments and play a key role in the decay of superfluid turbulence. Certain filaments can also support non-linear solitary waves, which are spatially confined excitations that maintain a constant amplitude. For vortex filaments in fluids, such solitary waves were theoretically predicted in the 1970ies by Hasimoto and subsequently observed experimentally.
Strings of a different kind arise in cubic chiral magnets like MnSi, FeGe or Cu2OSeO3. Here, the competition between exchange and Dzyaloshinskii-Moriya interactions stabilises magnetic skyrmions, i.e., two-dimensional topological textures of the magnetization. These skyrmions extend along the third direction forming topological strings. In a recent theoretical work, researchers from our institute demonstrated that such skyrmion strings also support solitary waves. Analytical results derived with the help of an effective field theory were successfully confirmed by numerical simulations. Interestingly, in the limit of low-energy the effective field theory approximately coincides with the integrable theory of Hasimoto suggesting that the solitary waves of the skyrmion strings are approximate solitons.